How Is the Isoptic Calculated?
How Is the Isoptic Calculated?

When designing an architectural space, it’s necessary to think about how to satisfy the needs of each user, looking to achieve an adequate level of comfort and a pleasant experience. Auditoriums, cinemas, and theatres are spaces that involve large masses of people, so special attention must be paid to factors like isoptics, acoustics or accessibility so that when witnessing an event, everyone is able to receive the same information.

Beyond the regulations imposed in each region or the characteristics of each project, the isoptic calculation allows us to know the curve drawn to achieve adequate public visibility at a given event. Taking into consideration that the human eye has a visual field of 180°, it is recommended to project based on the pertinent measurements and angles that will allow all the observers to have full visibility of the show.

Both the vertical and horizontal isoptics present certain margins of effective use with respect to the viewers’ vision upon a point of interest. If we go back in time, it is since Greek times that it was believed that the best way to address this problem was through a circular arrangement, which is the reason why so many infrastructures have been designed this way. Nowadays, there are multiple morphologies and dispositions that have been able to be implemented in these spaces based on in-depth studies and research. Here, we present some of the fundamental principles to keep in mind when projecting them.
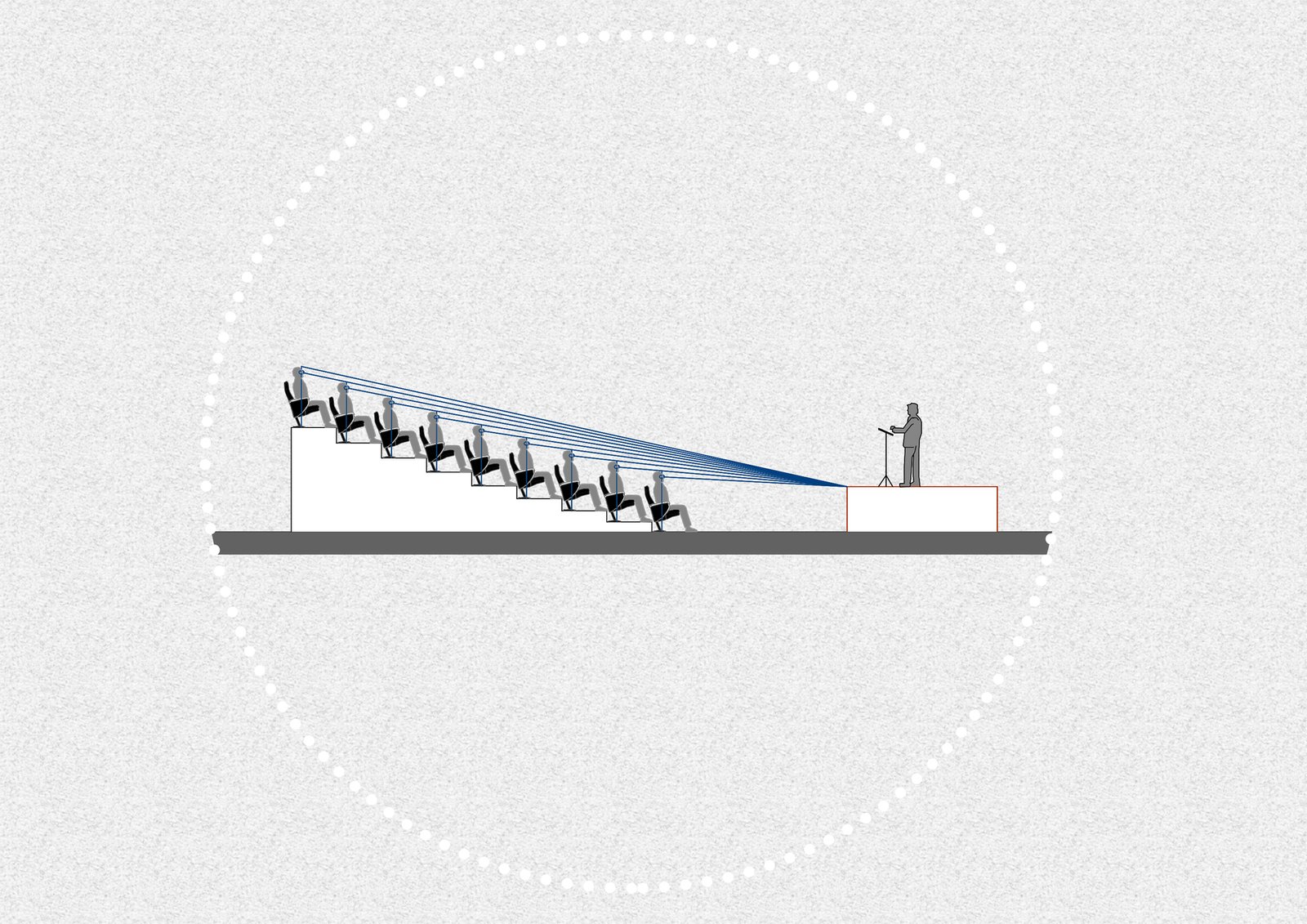
Vertical isoptic

The aim of the vertical isoptic is to find the most convenient heights/slopes for the design of the stands. Its calculation defines the ascending curve that creates the staggering of the floors between the rows of observers, which allows for good visibility. Through mathematical methods, the isoptic trace can be obtained with the following formula, where h´ is the height of the spectator’s eye, d´ is the distance between the spectator and the base point for the trace, h is the height of the spectator’s eyes from the row before the one being calculated, k is a constant that indicates the difference in level between the eyes and the top of the head, and d is the distance between the base point for the trace and the spectators seated in the row before the one being calculated.
h´= (d´(h+k) ) / d
In addition, there are other variables to take into account such as the anthropometry of the people considered as users, the type of furniture to be placed, or even if the spectators are standing or not. When dealing with seated spectators, the average height from the person’s eyes to the ground is considered to be approximately 1.10 metres, with the distance between the ear and the top of the head (k) being approximately 12 cm.

For the calculation, it is proposed to establish a distance of 3 metres between the stage and the first row of seats located above level zero and a depth of 0.70 metres to define the position of the person in their seat. The procedure consists of placing a point that symbolises the head of the first observer on their seat, taking a distance (d) of 0.90 metres as the separation between the rows of the stands. Then, an observation reference point called F is installed that fulfils the role of the lower limit of the visual field and is also 0.90 metres from the ground. A straight line is drawn and the isoptic curve is started. Another point will be placed at a height k and a new straight line will be drawn from that point to point F, to be continued until the intersection with the next vertical line that represents the next spectator. This way, all the lines are drawn from point F to the successive vertical lines and the stands are drawn taking into account the lower limit of the distance of 1.10 metres.
Horizontal isoptic

The horizontal isoptic determines the radial distribution of the seats on the horizontal plane allowing for optimal lateral vision. When talking about field of vision, it refers to the proportion of space measured in degrees and perceived by keeping the head and eyes fixed on an object. When contemplating with both eyes, the fields of vision overlap and the central field is even greater, achieving an amplitude of 60°. It is important to consider both the width of the seats and the regulations according to the use of the site, and the kind of show to be developed since all of this affects the distribution typology.
By establishing a point P that corresponds to twice the width of the front of the stage, a line is drawn from it to points A and B that represent the limits of the stage. It is necessary that the central point of the first row towards points A and B has an angle of 110°, while the last row of seats should limit the view of the central spectator to an angle of 30°.